There has been a major structural shift in financial markets since the 1980s. The world is awash in credit, and credit is cheaper than ever before. I discuss how increasing financial surpluses within parts of the economy have resulted in an expansion in the supply of credit, which has largely financed the demand-side of the real economy. This increasing reliance on “credit as demand” raises some serious policy questions going forward. I discuss the importance of equitable and inclusive growth, fair taxation system and risk-sharing in creating a financial system that promotes prosperity and stability.
The big shift in finance
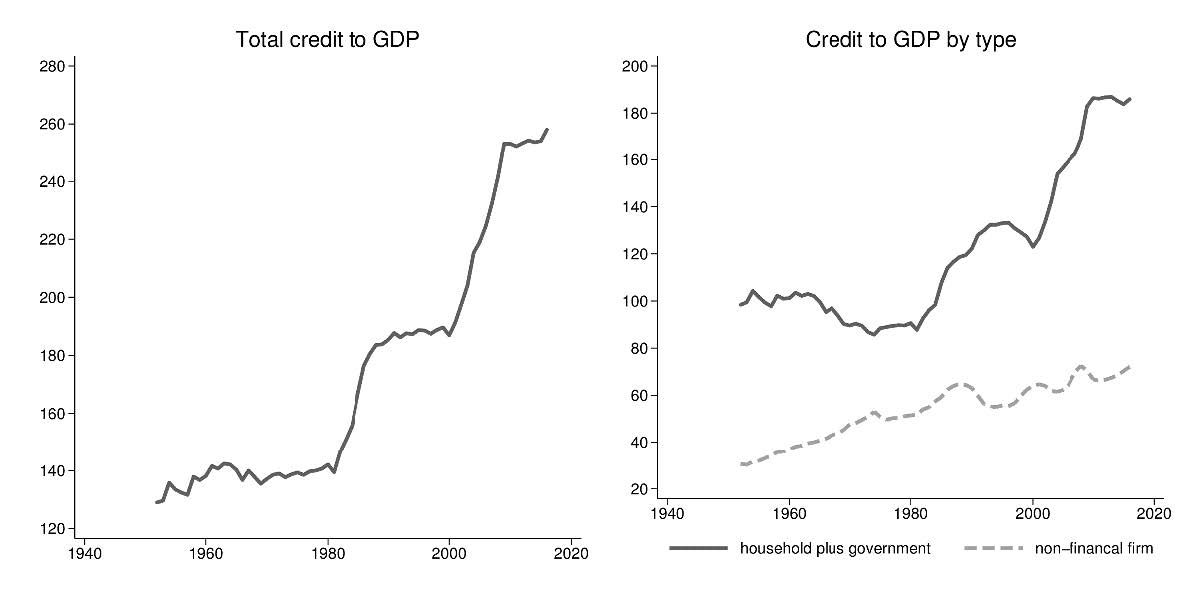
The left panel of figure 1 shows that total credit in the U.S. remained relatively flat at around 140% of GDP in the post-war years until 1980. Since 1980, however, credit has gone up at a rapid pace, reaching a historic high of 258% of GDP in the most recent numbers available for 2016 [1]. Even the great recession did not put much of a dent in the growth of credit, with total credit rising from 232% in 2007 to 258% in 2016.
The phenomenal rise in credit is in fact a global phenomenon as the work of Oscar Jorda, Moritz Schularick and Alan Taylor has carefully documented. The recently released global debt database from the IMF that covers both advanced and emerging economies also shows a big increase in global credit to GDP from around 150% between 1960 and 1980 to over 250% in 2016.
The right panel of figure 1 splits total credit into non-financial firm credit and credit going to households plus government. The figure shows that most of the increase in credit since 1980 has been driven by credit going to households and the government. Credit going to the corporate sector plays a relatively minor role in explained the big rise in total credit. In particular, 82% of the increase in total credit as a share of GDP sine 1980 is driven by credit going to households and the government. The big increase in total credit, especially credit going to households and government, is not unique to the U.S. Jord`a et al. (2016) show that there has been a large increase in private bank credit in all advanced countries since 1980. The authors further show hat the increase in credit is dominated by mortgage credit going to the household sector.
Figure 1 Big shift in finance
The large increase in credit has been accompanied by a persistent decline in the price of credit as long term interest rates have fallen to historic lows. For example, the average 10-year real interest rate has declined from a high of 6% in 1983 to zero in recent years (IMF WEO (2014)). The fall in the price of credit even as the quantity of credit exploded suggests that the expansion in financial sector is driven by an increase in the “supply” of credit. What is behind this structural shift in finance?
The United States, and the global economy, experienced a couple of major structural shifts around 1980. First, share of income going to the top 1% of earners went up significantly. The richest 1% of Americans captured 11% of total income in 1980 and 20% in 2014 (Piketty and Saez (2003)). The rise in top income share occurred in many other countries as well (see e.g. Alvaredo et al. (2018)). Second, the collapse of the Bretton Woods system in 1971 ushered in the era of global capital flows. A number of countries started running large current account deficits or surpluses post 1980. High savings by oil-rich countries and high-growth Asian economies have also contributed to the global rise in credit through cross-border flows that have accelerated since 1980. The U.S. had close to a balanced current account in 1980 but has been consistently running current account deficits of over 2% of GDP since then.
The rise in top income share contributes to the expansion of the size of the financial sector. High-income earners save a large share of their income, creating a larger “financial surplus” within the economy that is then channeled back through the financial sector. The financial sector deploys these larger gross savings back into the economy through credit creation. There is a close association between the rise in top-income share of the top 1% and the rise in household leverage for the rest of the population, suggesting that increased gross savings from the top 1% were partly absorbed by increased borrowing by the remaining household sector.
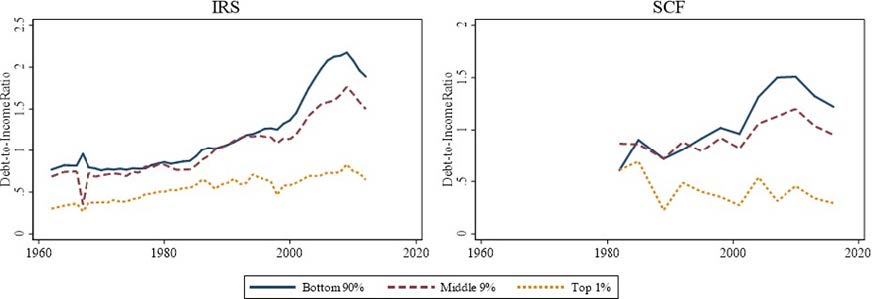
Figure 2 shows the evolution of debt to income for the top 1%, middle 9% and the remaining bottom 90% in both IRS and SCF data sets. The rise in household credit is concentrated in the bottom 99% and not the top 1%, while income gains since 1980’s have largely gone to the top 1%. Mian and Sufi (2018) show the same pattern holds when using individual level credit bureau data.
Figure 2 Debt-to-income ratio across the income distribution
What has the increased credit supply financed? The “credit as demand” channel
The increasing financial surpluses, or savings gluts, have expanded the total supply of credit to the economy, lowering long-term interest rate in the process. What has the increased supply of credit financed?
The textbook model of finance says that credit is used to finance real investment: savers deposit their surplus funds in the banking sector which then lends these funds to firms for investment. In other words, credit is used to finance production, or the supply-side of the economy. However, evidence suggests that a relatively small fraction of the increase in credit has gone towards funding production. For example, despite the large increase in credit creation, rate of investment has not gone up. The average U.S. gross investment rate was 22.5% from 1947 through 1979 and 21.8% from 1980 onwards.
Other evidence is also at odds with the idea that the additional credit has gone into increasing productive capital. Overall growth is not any higher post-1980. Moreover, there is strong evidence that productivity growth has slowed down significantly over the last decade and a half. If additional credit has not gone into financing production as much, then the other possibility is that credit has increasingly been used to fund demand. There is indeed robust evidence to support this view.
I have already shown that most of the increase in credit since 1980 has been used to fund government fiscal deficits, or household financial deficits, especially households outside of the top 1%. The concentrated growth in government and household debt suggests that aggregate demand is increasingly reliant on credit creation for support.
The reliance on credit creation for supporting aggregate demand is a natural consequence of a higher share of income being saved due to increased inequality. Equilibrium condition for the real economy implies that as a larger fraction of the output is saved, the increased savings must be channeled back to the real economy either as investment or consumer demand. In the absence of such a channel, the real economy will be forced to contract – or not grow as fast – in order to equate supply and demand in the real economy. This phenomena is sometimes referred to as “liquidity trap” or “savings trap” in the literature (e.g. Eggertsson and Krugman (2012)).
Theoretically, as long as certain sectors within the economy such as the government or households below the top 1% are willing to run larger deficits, the real economy can continue to grow at full capacity. However, as the economy continues to rely on credit-creation for supporting demand, it becomes increasingly more difficult to do so. The reason is that as household and government credit builds up, interest rate needs to fall in order to keep the debt service requirement manageable. The reduction in interest rate also tends to raise asset prices, especially housing values, which enables household to borrow more easily. But the dependence on ever lower interest rate to support a larger stock of debt cannot go on forever.
At some point it becomes difficult for interest rate to drop any further without adding a cost of its own. First, there is the natural zero lower bound constraint on nominal interest rate. Second, and perhaps more importantly, very low interest rates introduce other problems that are damaging for the overall economy. For example, asset markets are more prone to bubbles at very low interest rate. It becomes increasingly difficult to fund pension plans and insurance funds with long-dated liabilities.
The combination of high debt and increased likelihood of bubbles makes financial sector more fragile. Low interest rates can also inhibit productivity growth due to greater misallocation of capital (Gopinath et al. (2016)) or increased market concentration (Liu et al. (2018)).
Long-run policy implications
The remarkable growth in credit and the accompanying fall in long-term interest rate since 1980 represents the most important shift in finance in the modern era. The discussion above highlights why this shift is not sustainable, at least not without major harm to economic growth. A reliance on continuous credit creation to generate demand eventually slows down economic growth through liquidity trap like scenarios and other ill effects of very low interest rates.
What can be done to reduce the dependence on credit and create more space for economic growth as a result? As I mentioned, the root causes of secular credit growth lie in large financial surpluses in the economy that are then channeled through the financial system. A reversal of excessive credit dependence requires that financial surpluses be brought down to healthier levels. There are three types of structural changes in the economy that can help reduce the dependence on credit creation for aggregate demand.
First, more equitable growth will reduce the excessive savings that are accumulated by the top 1%. As explained above, there is a direct relationship between highly skewed economic growth and a bloated financial sector that results in broader economic malaise. Second, estate taxes and wealth tax (e.g. as proposed by Piketty (2014)), especially on “money-like” instruments[2], can be useful in restraining excessive surpluses. Some of the revenue raised from wealth and estate taxes can be used to lower income taxes for lower income brackets that have a high propensity to spend. Third, high inter-generational mobility helps to reduce the adverse effects of financial surpluses as accumulated surpluses naturally get liquidated across generations. Thus policies that strengthen public education and provide more equitable opportunities to the entire population help reduce dependence on credit creation.
Cyclical and more immediate policy implications
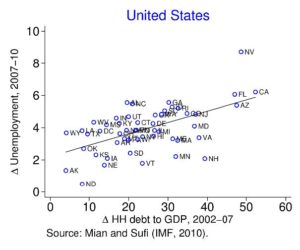
I next turn my attention to more immediate steps that can be taken to reduce the cyclical costs of problems emanating from financial markets. The most striking empirical regularity connecting credit and business cycles in recent decades is that large run up in credit, especially household credit, tends to be followed by an increase in unemployment. The 2008 global crisis, as shown in figure 3, was one manifestation of this broader trend. States within the U.S. that had a larger increase in household leverage between 2002 and 2007, ended up experiencing a much more severe recession. Remarkably, we find exactly the same relationship across countries.
Figure 3 Credit growth and recessions
 |
 |
In Mian and Sufi (Forthcoming), we explain how recurrent business cycle contractions such as the one in figure 3, are the result of “credit-driven household demand channel”. The basic idea is that expansion in the supply of credit fuels a boom in credit and asset prices that boosts household aggregate demand. However, the expanding credit boom also sows the seeds of its own destruction and ultimately results in a macroeconomic slowdown.
How should policy be tailored to address such credit-induced boom-bust cycles? I discuss steps regarding macro-prudential policy, tax policy, banking regulation, GSE reforms, and bankruptcy law that help reduce the likelihood and adverse consequences of credit-induced boom-bust cycles. On the macro-prudential front, the most important policy focus should be to facilitate better risk-sharing between creditors and borrowers. Credit creates problems for the macro-economy in the event of a downturn due to differences across creditors and debtors in their marginal propensity to spend. A downturn naturally hurts borrowers disproportionately more since they are levered. Borrowers are also more sensitive to shocks as they tend to have much higher propensity to respond to shocks. The combination of these two forces implies that for any given macro shock, headwinds faced by the macro economy are stronger the more levered the economy is. Moreover, households may not fully internalize the possibility of such headwinds when deciding how much leverage to undertake. This results in economies getting “over-leveraged” with deeper and more frequent recessions.
A natural solution to minimizing the disruptions caused by credit is to promote ‘state-contingent contracting’ that allows a more equitable sharing of downside risk between creditor and debtor in the event of a macro downturn. The creditor will naturally be compensated for sharing downside risk upfront. State-contingent contracting does not suffer from the usual moral hazard problem in risk-sharing contracts, because the risk-sharing is contingent upon a macro state of nature over which the borrower has no direct control.
There are multiple examples of state-contingent contracts that have been proposed in the past. For example, sovereign debt repayment can be linked to GDP as proposed by Robert Shiller. Student debt repayment can linked to the earning potential of a graduating student’s cohort and major. We proposed a state-contingent “shared responsibility mortgage” (SRM) in our book Mian and Sufi (2014). SRM works by reducing monthly mortgage payments in the event of a local downturn in housing market without altering the amortization schedule – effectively providing both cash-flow and principal relief for borrowers.
The promotion of state-contingent contracts will have multiple advantages at the macro level. First, it will significantly reduce real macroeconomic volatility through the introduction of automatic stabilizers as debtors and creditors share risk more efficiently. Economic volatility is especially harmful for lower income households with more fragile economic conditions. Second, it will raise total welfare by avoiding long period of times when economy operates below capacity due to the after effects of debt overhang. In this way an economy with state-contingent contracting is both more resilient and stronger. Empirical evidence coming out of the Great Recession shows that better risk-sharing between debtors and creditors would have significantly reduced the extent and scale of the recession. Di Maggio et al. (2017) show that lower interest rates post-2008 were not passed-through to many constrained households who were unable to refinance, thus putting a real drag on aggregate demand[3]. Ganong and Noel (2017) show that reduction in mortgage payments undera government program significantly increased spending and lowered defaults. More than fourmillion homes were foreclosed over a short period of time during the Great Recession. Mian et al. (2015) show these fire sales put further downward pressure on house prices, thus worsening an already bad situation. State-contingent mortgages would have helped reduce the number of homes going into foreclosure.
A natural question that arises is that if state-contingent contracts are so beneficial, why do we not see more of them around us? There are three main reasons for this. First, the argument in favor of state-contingent contracting is based on the negative macro externalities inherent in standard debt contracts. Private agents, for both rational and behavioral reasons, are not likely to internalize these externalities. There is thus a rationale for promoting state-contingent contracting as part of macro-prudential policies. Second, as Admati et al. (2018) point out, shareholders have an incentive to ratchet leverage up since some of the benefits of reducing leverage accrue to creditors and not shareholders. Third, there are a number of institutional features in the U.S. and abroad that hinder the adoption of state-contingent contracting. I discuss specific policy steps that remove such obstacles and encourage adoption of state-contingent contracts.
The U.S. tax system offers an interest expense deduction that reduces the effective cost of debt financing for homeowners. The tax subsidy is naturally capitalized in people’s housing decisions and the value of the housing market. The tax subsidy distorts the financial system by encouraging leverage that is harmful from a macro-prudential perspective. Removing the tax subsidy is not feasible politically, and doing so may also depress the housing market. Therefore, we proposed in Mian and Sufi (2014) that the subsidy be moved over towards state-contingent contracts like the SRM that have nice macro-prudential characteristics. The current system not only subsidizes the housing sector, but does so in a way that is harmful from a prudential perspective.
Bank capitalization rules under the Basel system are also structured to discourage banks from holding state-contingent securities in their portfolio. For example, suppose a bank issues a traditional mortgage of 100,000$ with 80% loan to value ratio. How much capital does the bank need to issue this mortgage? The typical capitalization requirement is 8%, implying the bank needs 8,000$ of capital. However, Basel rules would give this mortgage a “risk weight” of 0.3, meaning that the bank only needs to cover 0.3 times the 8%, or 2,400$ in capital.
Now imagine the bank issued the same mortgage as an SRM. The risk weight would increase substantially, probably close to 1. As a result, the bank would need to have 8,000$ in capital, instead of the 2,400$, to issue the mortgage as an SRM. The higher capital requirement for state-contingent contracts is unfortunate and somewhat ironic from a societal view point.
The banking system is designed to discourage banks from holding state-contingent contracts that are more beneficial from a macro perspective. The premise behind banking regulations such as Basel III is that losses must be minimized for the banking sector, or creditors at large. The banking system is therefore encouraged to originate the “safest” of assets from the creditors’ perspective, and pass on all risk of debtors. However, as I have already explained, doing so leads to much worse outcomes in the event of a cyclical downturn. The current structure of banking regulation does not split risk between creditors and debtors in a socially beneficial manner.
The adoption of a new “standard” in financial markets often requires the government to step in and define new rules. For example, there is now an active and liquid market for inflation-indexed treasuries or TIPS. But that market was created by the U.S. government itself under Clinton administration. Similarly, the 30-year fixed rate mortgage became the standard mortgage in the U.S. after the government actively encouraged it. Today government-sponsored entities (GSEs) are by far the largest players in the mortgage origination business. The explicit government support enjoyed by ‘conforming’ mortgages supported by the GSEs means that it is more difficult for the private sector to introduce new solutions like state-contingent mortgages.
Given the existing large role of government in mortgage origination and the societal benefits associated with state-contingent contracts such as SRMs, the government could include state- contingent mortgages in its definition of ‘conforming’. The government could also help in defining states of the world, such as official local house price indices, to promote state-contingent mortgages. State-contingent contracting is an example of ex-ante macro prudential intervention. If properly implemented, it has the virtue of endogenously reducing economic volatility and crises, and hence the need for ex-post intervention in the first place. However, to the extent ex-post intervention is needed, efficient bankruptcy laws help in dealing with debt-overhang. The U.S. has better bankruptcy laws compared to rest of the advanced world, especially for households. However, there are certain areas, such as student loans, where bankruptcy laws need to be amended to enable restructuring of odious student debt.
The broader message to take-away is that risk-sharing between creditors and debtors is an important principle to promote. Macro-prudential and regulatory policies should be designed to favor risk-sharing. Unfortunately the current tax and regulatory system is designed to do the opposite. The present regulatory regime is “bank-centric”, with an exclusive focus on minimizing default probability for banks. This is short-sighted and does not take into account the true cost for the real economy when the financial system passes risk squarely on debtors. The banking sector should be better capitalized, as argued forcefully by Admati and Hellwig (2013), with a capital structure that is more suited to absorbing losses without going into bankruptcy.
Endnotes
[1] Total credit includes private credit (household debt and non-financial firm debt) and sovereign credit.
[2] This would be akin to having a negative interest rate on some margins in the current environment.
[3] For broader evidence on household demand channel constraining the efficacy of monetary policy, see Agarwal et al. (2017,2018); Aladangady (2014); Baker (2018); Cloyne et al. (2017); Jordà et al. (2014)